Skip to contents

Poisson time-series model.

Source: R/estimator-locfit.R
poisson_locfit_model.Rd

Takes a list of times and counts and fits a quasi-poisson model fitted with a log link function to count data using local regression using the package locfit.

Usage

poisson_locfit_model(
  d = i_incidence_input,
  ...,
  window = 14,
  deg = 2,
  frequency = "1 day",
  predict = TRUE,
  ip = i_discrete_ip,
  quick = FALSE,
  .progress = interactive()
)

Arguments

d

input data - a dataframe with columns:

  • count (positive_integer) - Positive case counts associated with the specified time frame

  • time (ggoutbreak::time_period + group_unique) - A (usually complete) set of singular observations per unit time as a `time_period`

Any grouping allowed.

...

not used and present to allow proportion model to be used in a group_modify

window

a number of data points defining the bandwidth of the estimate, smaller values result in less smoothing, large value in more. The default value of 14 is calibrated for data provided on a daily frequency, with weekly data a lower value may be preferred. - default 14

deg

polynomial degree (min 1) - higher degree results in less smoothing, lower values result in more smoothing. A degree of 1 is fitting a linear model piece wise. - default 2

frequency

the density of the output estimates as a time period such as 7 days or 2 weeks. - default 1 day

predict

result is a prediction dataframe. If false we return the locfit models (advanced). - default TRUE

ip

An infectivity profile (optional) if not given (the default) the Rt value will not be estimated - a dataframe with columns:

  • boot (anything + default(1)) - a bootstrap identifier

  • probability (proportion) - the probability of new event during this period.

  • tau (integer + complete) - the days since the index event.

Minimally grouped by: boot (and other groupings allowed).

A default value is defined.

quick

if ip is provided, and quick is TRUE Rt estimation will be done assuming independence which is quicker but less accurate. Setting this to false will use a full variance-covariance matrix.

.progress

show a CLI progress bar

Value

A dataframe containing the following columns:

  • time (ggoutbreak::time_period + group_unique) - A (usually complete) set of singular observations per unit time as a time_period

  • incidence.fit (double) - an estimate of the incidence rate on a log scale

  • incidence.se.fit (positive_double) - the standard error of the incidence rate estimate on a log scale

  • incidence.0.025 (positive_double) - lower confidence limit of the incidence rate (true scale)

  • incidence.0.5 (positive_double) - median estimate of the incidence rate (true scale)

  • incidence.0.975 (positive_double) - upper confidence limit of the incidence rate (true scale)

  • growth.fit (double) - an estimate of the growth rate

  • growth.se.fit (positive_double) - the standard error the growth rate

  • growth.0.025 (double) - lower confidence limit of the growth rate

  • growth.0.5 (double) - median estimate of the growth rate

  • growth.0.975 (double) - upper confidence limit of the growth rate

Any grouping allowed.

Details

This results is an incidence rate estimate plus an absolute exponential growth rate estimate both based on the time unit of the input data (e.g. for daily data the rate will be cases per day and the growth rate will be daily).

Examples



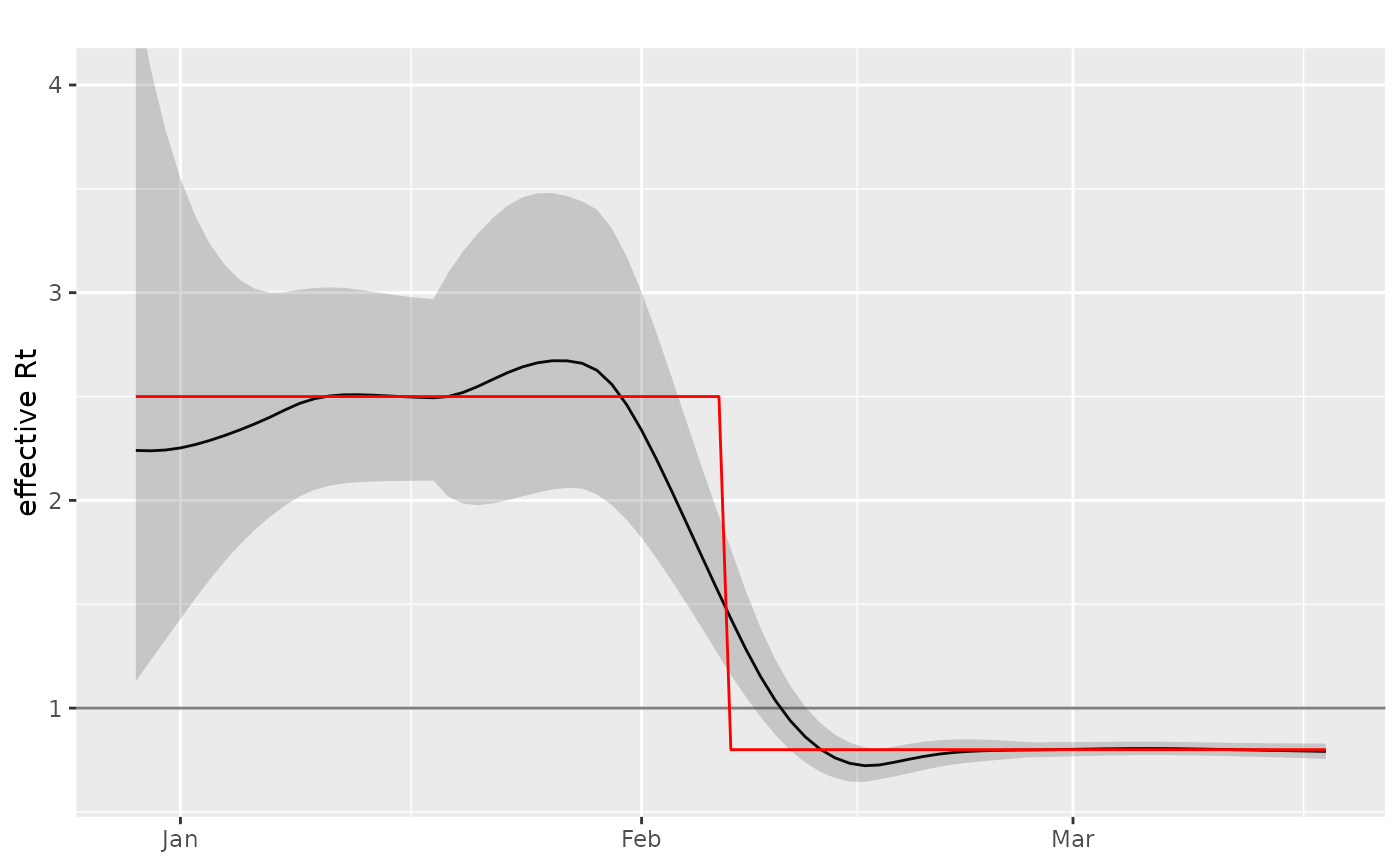
data = test_poisson_rt
tmp = data %>% ggoutbreak::poisson_locfit_model(window=14,deg=2, ip=test_ip, quick=TRUE)
#> Rt estimation using Locfit (approx and assuming independence)
#> Warning: Estimates were assumed to be independent, but more that 1% of estimates
#> are at risk of Rt underestimation by more that 0.05 (absolute).
#> We advise re-running supplying a full variance-covariance matrix, or
#> a value to the `raw` parameter, or setting `quick=FALSE`.
plot_rt(tmp)+sim_geom_function(data,colour="red")


data = test_poisson_growth_rate
tmp2 = data %>% ggoutbreak::poisson_locfit_model(window=7,deg=1)
tmp3 = data %>% ggoutbreak::poisson_locfit_model(window=14,deg=2)



comp = dplyr::bind_rows(
  tmp2 %>% dplyr::mutate(class="7:1"),
  tmp3 %>% dplyr::mutate(class="14:2"),
) %>% dplyr::group_by(class)

if (interactive()) {
  plot_incidence(
    comp,
    date_labels="%b %y",
    raw=data
  )+
  ggplot2::geom_line(
    data=data,
    mapping=ggplot2::aes(x=as.Date(time),y=rate),
    colour="grey40"
  )

  plot_growth_rate(
    comp,
    date_labels="%b %y"
  )+
  sim_geom_function(data,colour="black")
}